Çinli Bilim İnsanlarından Matematik Dünyasını Sarsan Çözüm
Matematik alanında uzun süredir çözülememiş bir soruna ilişkin önemli bir gelişme yaşandı. Pekin Üniversitesi’nin değerli mezunu olan Xu Zhouli, birlikte çalıştığı Wang Guozhen ve Lin Weinan adlı matematikçiler, yaklaşık 65 yıldır matematik camiasını meşgul eden ve yanıtı bulunamayan bir problemi nihayet çözerek ispatlamayı başardılar. Bu büyük başarının odağında yer alan mesele, Kervaire değişmezi veya diğer adıyla Kervaire invariant olarak bilinen, karmaşık ve derin bir konu. Peki, bu mesele nedir ve neden bu kadar önemlidir? İşte detaylar…
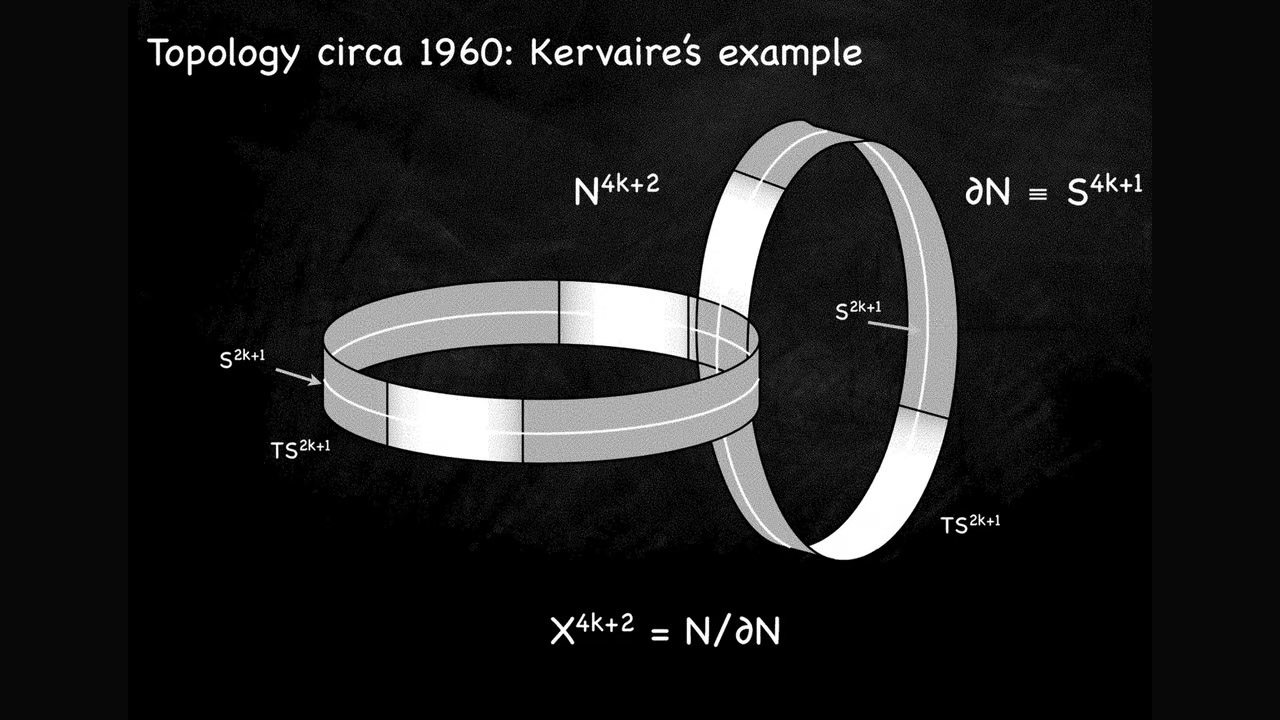
Kervaire değişmezinin temel anlamı ve önemi
Kervaire değişmezi, aslında bir fonksiyon türüdür. Bu fonksiyonun temel görevi, bir topolojik şeklin veya manifoldun, “cerrahi” adı verilen özel matematiksel işlemlerle küreye dönüştürülüp dönüştürülemeyeceğini ölçmektir. Eğer şekil, bu işlemler sonunda küreye dönüşebiliyorsa, fonksiyonun sonucu sıfır olur; dönüşemiyorsa, sonuç 1 olur. İşte bu fonksiyonun değeri, şeklin belirli boyutlarda küreye dönüşüm kabiliyetini gösterir. Bu bağlamda, 126. boyutta da yapıldığı gibi, sonucu 1 olan boyutların sayısı artmaya devam ediyor. Bu gelişme, matematik dünyasında büyük yankı uyandırdı ve önemli bir dönüm noktası oldu.
Çalışmaların tarihçesi ve yeni keşif
Yıllar boyunca, matematikçiler, hangi boyutlarda bu fonksiyonun sonucu 1 olur sorusuna cevap aradılar. İlk olarak, 1964 yılında 2. boyut ve ardından 6 ve 14. boyutlar üzerinde bu sonuca ulaşılırken, 1984 yılında ise 30 ve 62. boyutlar için bu durum tespit edildi. Yani, matematikçiler, belirli boyutlarda bu fonksiyonun sonucu 1 olabileceğine dair kanıtlar elde etmişlerdi. Fakat, aradan geçen zaman içinde, 126. ve 254. boyutlar gibi daha büyük boyutlarda bu sonucun ne olacağı kesin olarak bilinmiyordu. İşte bu noktada Çinli bilim insanları devreye girdi ve 126. boyutta da bu sonucun 1 olduğunu gösteren güçlü bir ispat sundular. Bu, matematik alanında oldukça büyük bir gelişmedir ve uzun süredir beklenen bir aşamayı temsil etmektedir.
İspat süreci ve kullanılan yöntemler
Başarının arkasında yatan temel yöntemler ise, geleneksel matematiksel tekniklerin yanı sıra bilgisayar destekli hesaplamalar olmuştur. Xu Zhouli, Wang Guozhen ve Lin Weinan, son derece karmaşık olasılıkları ve olasılıkların kontrolünü sağlamak amacıyla toplamda 105 farklı olasılığı detaylı şekilde incelediler. Bu süreç, onların bilgisayar sistemlerinden aktif şekilde yardım almasıyla mümkün oldu. Bu çalışmalar sırasında, tüm olasılıkları tek tek ele alıp eleyerek, sonuca ulaşmayı başardılar. Ancak, şu an itibariyle bu çalışma, hakem onayı almadı ve resmi kabul süreci devam ediyor. Onay alındığı takdirde, bu gelişmenin matematik dünyasında büyük yankılar uyandırması bekleniyor.
Geleceğe dair umutlar ve olası etkiler
Bilim insanları, bu yeni yöntemlerin ve elde edilen sonuçların, diğer çözülememiş problemlerde de kullanılabileceğine inanıyorlar. Eğer bu teknikler, farklı alanlarda da uygulamaya konursa, matematik ve topoloji gibi disiplinlerde büyük sıçramalar yaşanabilir. Bu gelişmeler, matematiksel araştırmalara yeni ufuklar açacak ve bilim dünyasında yeni bir dönemi başlatabilir. Ayrıca, Kervaire değişmezine ilişkin bu başarının, diğer karmaşık problemlerde kullanılma potansiyeli, alanın geleceği açısından oldukça umut verici.
Sonuç ve kaynaklar
Bu büyük gelişmenin detaylarına ve bilim insanlarının çalışmalarına ulaşmak için aşağıdaki kayda değer kaynağı inceleyebilirsiniz:



